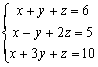
СpЅпЄG/ЄTЄИЄ@ІИЄшЕ{(Ѕ]ЌAГqИб)ЄЮІцІCІЁ(II)
Е{ІЁЈЯЅЮЄFЇJЕмКПЊkЋh (Cramer's rule)ЁAІ]ІЙИћЄ@ЏыЈЯЅЮЎјЅhЊkЊКЕ{ІЁЁAЗЧНTЋзДЃАЊЄFЁAІгЅBЕ{ІЁЊКЈюБјЅѓЅчИћЄжЁCЕ{ІЁАЃЄFЅiЅHpКтСpЅпЄTЄИЄ@ІИЄшЕ{ЊКЎкЄЮІцІCІЁЅ~ЁAСйЅiЅHpКтСpЅпЄTЄИЄ@ІИЄшЕ{ЊКГqИбЄЮСpЅпЄGЄИЄ@ІИЄшЕ{ЊКЎк ЁCЕ{ІЁСіЕMИћВФ(I)ЊЉЊјЄ@ТIЁAІ§ГqИбЈЯЅЮЄFЄ@ЏъВпКDЊКЄшЊk(z=t)ЁAЅtЅ~Е{ІЁЇѓЅiЅHАtІXЄpМЦТрДЋЄРМЦЕ{ІЁ(III)ЊКВФЄGгЕ{ІЁБNЄшЕ{ЊКИб(Ѕ]ЌAГqИб)ТрЄЦЌАЄРМЦЁC
Е{ІЁНsМgЄщДС: 2007І~2Єы3Єщ
Е{ІЁ(116ЈB)
| 1 | ENT | 2. | Kin 2 | 3. | ENT | 4. | Kin 1 | 5. | Kin 5 |
| 6. | ENT | 7. | Kin 3 | 8. | ENT | 9. | Kin 4 | 10. | ENT |
| 11. | + | 12. | ( | 13. | ENT | 14. | Kin 6 | 15. | Ёб |
| 16. | Kout 3 | 17. | - | 18. | ENT | 19. | Kin Ёб 5 | 20. | XЁіЁїK5 |
| 21. | ) | 22. | +/- | 23. | Min | 24. | 0 | 25. | = |
| 26. | Kin Ёб 3 | 27. | XЁіЁїK2 | 28. | Kin Ёб 5 | 29. | XЁіЁїK5 | 30. | Kin - 3 |
| 31. | Kout 5 | 32. | XЁіЁїK6 | 33. | Kin Ёб 6 | 34. | XЁіЁїK4 | 35. | Kin Ёб 4 |
| 36. | XЁіЁїK2 | 37. | Kin Ёб 2 | 38. | XЁіЁїK1 | 39. | Kin Ёб 1 | 40. | Ёб |
| 41. | Kout 1 | 42. | Kin - 6 | 43. | ENT | 44. | Kin Ёб 5 | 45. | = |
| 46. | Kin - 4 | 47. | Kout 2 | 48. | Kin - 5 | 49. | Kout 4 | 50. | Ёв |
| 51. | Kout 6 | 52. | = | 53. | ENT | 54. | Kin 1 | 55. | Ёб |
| 56. | MR | 57. | + | 58. | Kout 5 | 59. | XЁіЁїK6 | 60 | Kin Ёв 6 |
| 61. | XЁіЁїK6 | 62. | Kin 2 | 63. | ENT | 64. | Kin 2 | 65. | Ёб |
| 66. | Kout 3 | 67. | + | 68. | MR | 69. | XЁіЁїK6 | 70. | Kin Ёв 6 |
| 71. | XЁіЁїK6 | 72. | Min | 73. | ENT | 74. | Ёб | 75. | Kout 6 |
| 76. | = | 77 | XЁіЁїK4 | 78. | Kin Ёб 1 | 79. | XЁіЁїK2 | 80. | XЁіЁїK5 |
| 81. | Kin Ёб 5 | 82. | XЁіЁїK5 | 83. | Kin + 1 | 84. | Kout 3 | 85. | Ёв |
| 86. | Kout 6 | 87. | = | 88. | ENT | 89. | XЁіЁїK6 | 90. | Kin Ёб 6 |
| 91. | XЁіЁїK6 | 92. | Kin - 1 | 93. | Kout 4 | 94. | HLT | 95. | +/- |
| 96. | Kin Ёв 1 | 97. | Kout 1 | 98. | Kin Ёб 3 | 99. | Ёб | 100. | MR |
| 101. | Ёб | 102. | Kout 6 | 103. | = | 104. | Kin + 2 | 105. | Kout 5 |
| 106. | Kin + 3 | 107. | Kout 6 | 108. | Kin Ёв 3 | 109. | Kin Ёв 2 | 110. | Kout 2 |
| 111. | HLT | 112. | XЁіЁїK1 | 113. | XЁіЁїK3 | 114. | Kin 2 | 115. | HLT |
| 116. | Kout 3 | 117. | Ё@ | 118. | Ё@ | 119. | Ё@ | 120. | Ё@ |
LRN МвІЁПщЄJЕ{ІЁ(Јб fx-3600PVЄЮfx-3800PЈЯЅЮЁAЕ{ІЁЊјЋз: 116ЈB )
| ENT 1 | Kin 2 | ENT 1 | Kin 1 | Kin 5 |
| ENT 1 | Kin 3 | ENT 1 | Kin 4 | ENT 0 |
| + | ( | ENT 1 | Kin 6 | Ёб |
| Kout 3 | - | ENT 1 | Kin Ёб 5 | XЁіЁїK5 |
| ) | +/- | Min | 0 | = |
| Kin Ёб 3 | XЁіЁїK2 | Kin Ёб 5 | XЁіЁїK5 | Kin - 3 |
| Kout 5 | XЁіЁїK6 | Kin Ёб 6 | XЁіЁїK4 | Kin Ёб 4 |
| XЁіЁїK2 | Kin Ёб 2 | XЁіЁїK1 | Kin Ёб 1 | Ёб |
| Kout 1 | Kin - 6 | ENT 1 | Kin Ёб 5 | = |
| Kin - 4 | Kout 2 | Kin - 5 | Kout 4 | Ёв |
| Kout 6 | = | ENT 1 | Kin 1 | Ёб |
| MR | + | Kout 5 | XЁіЁїK6 | Kin Ёв 6 |
| XЁіЁїK6 | Kin 2 | ENT 2 | Kin 2 | Ёб |
| Kout 3 | + | MR | XЁіЁїK6 | Kin Ёв 6 |
| XЁіЁїK6 | Min | ENT 3 | Ёб | Kout 6 |
| = | XЁіЁїK4 | Kin Ёб 1 | XЁіЁїK2 | XЁіЁїK5 |
| Kin Ёб 5 | XЁіЁїK5 | Kin + 1 | Kout 3 | Ёв |
| Kout 6 | = | ENT 4 | XЁіЁїK6 | Kin Ёб 6 |
| XЁіЁїK6 | Kin - 1 | Kout 4 | HLT | +/- |
| Kin Ёв 1 | Kout 1 | Kin Ёб 3 | Ёб | MR |
| Ёб | Kout 6 | = | Kin + 2 | Kout 5 |
| Kin + 3 | Kout 6 | Kin Ёв 3 | Kin Ёв 2 | Kout 2 |
| HLT | XЁіЁїK1 | XЁіЁїK3 | Kin 2 | HLT |
| Kout 3 | MODE . | Ё@ | Ё@ | Ё@ |
Ељ: YЄшЕ{ВеЌА a1x + b1y + c1z = d1 , a2x + b2y + c2z = d2 , a3x + b3y + c3z = d3
Е{ІЁЊКЈюБјЅѓЌА: a1b2Ёкa2b1ЁAYЊGЄшЕ{ВеЊКІцІCІЁХуЅмЌАЙsЁAЊэЅмЄшЕ{ЕLАпЄ@Иб(ЕLИбЉЮЕLИб)ЁA Е{ІЁЗ|ІbХуЅмІцІCІЁМЦШЋсЅXВ{-E-ЁCYЊGЅuЌOПщЄJЊКМЦОкЙHЄЯЈюБјЅѓЁAЋhЗ|Іb ПщЄJВФЄGВеЄшЕ{ЋсЁAЕ{ІЁЄ~З|ЅXВ{-E-ЁAГoЎЩНаБNЄшЕ{ВеЄКЊКЄшЕ{ІЁНеДЋІИЇЧПщЄJЁC
Ё@
ЈвУD1: ИбСpЅпЄшЕ{ :
Ћі P1 ІAЋі 1 RUN 1 RUN 1 RUN 6 RUN 1 RUN 1 +/- RUN 2 RUN 5 RUN 1 RUN
3 RUN 1 RUN 10 RUN (Ѕ§ХуЅмЄшЕ{ВеІцІCІЁЊКШЌА - 2)
RUN (ХуЅмx=1) RUN (ХуЅмy=2) RUN (ХуЅмz=3)
Е{ІЁАѕІцЇЙІЈЋсACВзЄюЕ{ІЁЁAЋі Kout 1ЁBKout 2ЁBKout 3ЄЮKout 4ЄРЇOХуЅмxЁByЁBzЊКШЄЮЄшЕ{ВеІцІCІЁЊКШЁC
Ељ1: Е{ІЁЅiЅHАtІXЄpМЦТрДЋЄРМЦЕ{ІЁ(III)ЊКВФЄGгЕ{ІЁЁAБNСpЅпЄTЄИЄ@ІИЄшЕ{ЊКИбТрЄЦЌАЄРМЦЁCЊ`ЗN: ТрЄЦЎЩЁAНаЅ§ТрЄЦИбЕЊzШЁAТрЄЦЋс zШЊКАOОа(K3)ЄЮІцІCІЁЊКАOОа(K4)ЋhЄЃЏрЋOЏdЁAЄЇЋсІAЋі Kout 1(ЉЮKout 2)ДЃЈњ xЊКШ (ЉЮ yЊКШ) ТрЄЦЌАЄРМЦЁC
Ё@
ЈвУD2: ИбЅHЄUСpЅпЄGЄИЄ@ІИЄшЕ{
![]()
ПщЄJЎЩЅunЄЃПщЄJzЊКЋYМЦЇYЅi
Ћі P1 ІAЋі 1 RUN 1 RUN RUN (ЄЃПщЄJМЦШ) 7 RUN
1 RUN -1 RUN RUN (ЄЃПщЄJМЦШ) 1 RUN (ХуЅм4) RUN (ХуЅм3)
І]ІЙИбЕЊЌА x = 4 ЄЮ y = 3.
p
КтЇЙЕВЁAНаЋіACЄЄЄюЕ{ІЁ ЁAxЊКШЁByЊКШЄЮЄшЕ{ВеІцІCІЁЊКШЄРЇOРxІsЉѓАOОаK1ЁBK2ЄЮK6ЄЄЁCЕљ2: ІbВзЄюЕ{ІЁЋсЁAЅiБNИбЕЊТрЄЦЌАЄРМЦЁAЅiЋі Kout 1 (ЉЮ Kout 2)ДЃЈњ xШ(ЉЮ yШ)ЖiІцТрЄЦЇYЅiЁAІ§ІцІCІЁЊКАOОа(K6)ЋhЄЃЏрЋOЏdЁC
Ё@
ЈвУD3: pКтЄUІCЊКІцІCІЁ:Ё@
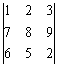
ПщЄJЎЩЅunЄЃПщЄJБ`МЦЖЕЇYЅi
Ћі P1 ІAЋі 1 RUN 2 RUN 3 RUN RUN (ЄЃПщЄJМЦШ)
7 RUN 8 RUN 9 RUN RUN (ЄЃПщЄJМЦШ)
6 RUN 5 RUN 2 RUN RUN (ЄЃПщЄJМЦШЁAХуЅмІцІCІЁЊКШЌА12)
Е{ІЁАѕІцЇЙІЈЋсЁAНаЋіACЄЄЄюЕ{ІЁЁCІцІCІЁЊКШРxІsЉѓАOОаK4ЁC
Ё@
ЈвУD4: ЈDЄUІCСpЅпЄшЕ{ЊКГqИб:
![]()
Ћі P1 ІAЋі - 7 RUN 1 RUN 1 RUN 3 RUN 1 RUN -1 RUN 1 RUN 1 RUN
(ХуЅм xЊКИбЁAБ`МЦЖЕЌА - 0.666666666)
RUN (ХуЅм yЊКИбЁAБ`МЦЖЕЌА -1.666666667)
RUN (ХуЅм xЊКИбЁAtЊКЋYМЦЌА 0.333333333)
RUN (ХуЅм yЊКИбЁAtЊКЋYМЦЌА 1.333333333)
І]ІЙГqИбЌА:
x = - 0.666666666 + 0.333333333 t
y = - 1.666666666 + 1.333333333 t
z = t
YЊGЄЃЅЮБNИбЕЊТрЄРМЦЁAНаЋі AC ВзЄюЕ{ІЁЁAЇ_ЋhЊНБЕАѕІцЄpМЦТрДЋЄРМЦ(III)Е{ІЁЅ§ТрЄЦГЬЋсЊКМЦШ(yЊКИб tЋYМЦ)ЁAЈфОlЄTгГqИбЊКМЦШЄРЇOАOІsІbK1ЁBK2ЄЮMЄЄЁAЅunДЃЈњМЦШІAЖiІцТрЄЦЇYЅiЁC
Ё@