聯立三元一次方程及行列式
程式使用了克萊瑪法則 (Cramer's rule),因此較一般使用消去法的程式,準確度提高了,而且程式的限制條件亦較少,更可以配合小數轉換分數(II)或小數轉換分數程式(III)的第二個程式將方程的解轉化為分數。
程式編寫日期: 2006年9月29日
程式(86步)
| 1 | ENT | 2. | Kin 2 | 3. | ENT | 4. | Kin 1 | 5. | Kin 5 |
| 6. | ENT | 7. | Kin 3 | 8. | ENT | 9. | Kin 4 | 10. | ENT |
| 11. | Kin × 5 | 12. | X←→K5 | 13. | Min | 14. | ENT | 15. | Kin 6 |
| 16. | × | 17. | Kout 2 | 18. | M- | 19. | ENT | 20. | Kin × 2 |
| 21. | X←→K3 | 22. | Kin × 5 | 23. | X←→K5 | 24. | Kin - 2 | 25. | Kout 5 |
| 26. | X←→K6 | 27. | Kin × 6 | 28. | X←→K4 | 29. | Kin × 4 | 30. | X←→K3 |
| 31. | Kin × 3 | 32. | X←→K1 | 33. | Kin × 1 | 34. | × | 35. | Kout 1 |
| 36. | Kin - 6 | 37. | ENT | 38. | Kin × 5 | 39. | = | 40. | Kin - 4 |
| 41. | Kout 3 | 42. | Kin - 5 | 43. | ENT | 44. | × | 45. | Kout 6 |
| 46. | +/- | 47. | - | 48. | ENT | 49. | Kin 3 | 50. | × |
| 51. | Kout 2 | 52. | - | 53. | ENT | 54. | Kin 1 | 55. | × |
| 56. | MR | 57. | = | 58. | X←→K4 | 59. | Kin × 1 | 60 | X←→K3 |
| 61. | × | 62. | Kout 5 | 63. | - | 64. | Kout 4 | 65. | ENT |
| 66. | × | 67. | Kout 6 | 68. | = | 69. | Kin + 1 | 70. | Kout 4 |
| 71. | Kin ÷ 1 | 72. | Kout 1 | 73. | Kin × 2 | 74. | HLT | 75. | × |
| 76. | MR | 77 | = | 78. | Kin + 3 | 79. | Kout 5 | 80. | Kin + 2 |
| 81. | Kout 6 | 82. | Kin ÷ 2 | 83. | Kin ÷ 3 | 84. | Kout 2 | 85. | HLT |
| 86. | Kout 3 | 87. | 88. | 89. | 90. |
LRN 模式輸入程式(供 fx-3800P使用,程式長度: 86步 )
| ENT 1 | Kin 2 | ENT 1 | Kin 1 | Kin 5 |
| ENT 1 | Kin 3 | ENT 1 | Kin 4 | ENT 1 |
| Kin × 5 | X←→K5 | Min | ENT 0 | Kin 6 |
| × | Kout 2 | M- | ENT 1 | Kin × 2 |
| X←→K3 | Kin × 5 | X←→K5 | Kin - 2 | Kout 5 |
| X←→K6 | Kin × 6 | X←→K4 | Kin × 4 | X←→K3 |
| Kin × 3 | X←→K1 | Kin × 1 | × | Kout 1 |
| Kin - 6 | ENT 1 | Kin × 5 | = | Kin - 4 |
| Kout 3 | Kin - 5 | ENT 1 | × | Kout 6 |
| +/- | - | ENT 2 | Kin 3 | × |
| Kout 2 | - | ENT 3 | Kin 1 | × |
| MR | = | X←→K4 | Kin × 1 | X←→K3 |
| × | Kout 5 | - | Kout 4 | ENT 4 |
| × | Kout 6 | = | Kin + 1 | Kout 4 |
| Kin ÷ 1 | Kout 1 | Kin × 2 | HLT | × |
| MR | = | Kin + 3 | Kout 5 | Kin + 2 |
| Kout 6 | Kin ÷ 2 | Kin ÷ 3 | Kout 2 | HLT |
| Kout 3 | MODE . |
例題1: 解聯立方程 :
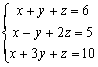
按 P1 再按 1 RUN 1 RUN 1 RUN 6 RUN 1 RUN 1 +/- RUN 2 RUN 5 RUN 1 RUN
3 RUN 1 RUN 10 RUN (顯示x=1) RUN (顯示y=2) RUN (顯示z=3)
程式執行完成後,按 Kout 1、Kout 2、Kout 3及Kout 4分別顯示x、y、z的值及方程組行列式的值。
例題2: 計算下列的行列式:
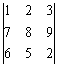
按 Prog 1 再按 1 RUN 2 RUN 3 RUN RUN (不輸入數值)
7 RUN 8 RUN 9 RUN RUN (不輸入數值)
6 RUN 5 RUN 2 RUN (這時會依然有"ENT",顯示行列式的值為12)
程式執行完成後,請按AC中止程式。行列式的值儲存於記憶K4。
註1: 若方程組為 a1x + b1y + c1z = d1 , a2x + b2y + c2z = d2 , a3x + b3y + c3z = d3
程式的限制條件為: b1c2≠b2c1,若果方程組的行列式顯示為零,表示方程無唯一解(無限解或無解), 程式會出現-E-。若果只是輸入的數據違反限制條件,則會在顯示第一個解答後,程式才會出現-E-,請將方程組內的方程式調換次序輸入。
註2: 程式會在輸入最後數據前顯示方程組行列式的值,若果不需要程式執行中顯示這個數值,紅色的程式 碼可以不輸入(程式長度變為85步),行列式的數值則需要自行按Kout 4顯示。
註3: 程式可以配合小數轉換分數(II)或小數轉換分數程式(III)的第二個程式,將方程的解轉化為分數。注意: 轉化時,請先轉化解答的z值,轉化後 z值的記憶(K3)及行列式的記憶(K4)則不能保留,之後再按 Kout 1(或Kout 2)提取 x的值 (或 y的值) 轉化為分數。