三階矩陣特徵多項式
程式編寫日期: 2006年12月21日
程式(90步)
| 1 | ENT | 2. | Min | 3. | Kin 3 | 4. | × | 5. | ENT |
| 6. | Kin 5 | 7. | ENT | 8. | Kin 4 | 9. | Kin 6 | 10. | ENT |
| 11. | Kin × 6 | 12. | Kin 1 | 13. | ENT | 14. | Kin 2 | 15. | - |
| 16. | ENT | 17. | Kin × 3 | 18. | X←→K3 | 19. | Kin - 6 | 20. | Kout 1 |
| 21. | × | 22. | Kout 5 | 23. | + | 24. | ( | 25. | Kout 6 |
| 26. | + | 27. | ( | 28. | Kout 5 | 29. | × | 30. | Kout 3 |
| 31. | - | 32. | Kout 2 | 33. | × | 34. | Kout 4 | 35. | + |
| 36. | ( | 37. | Kout 5 | 38. | + | 39. | ( | 40. | Kout 4 |
| 41. | × | 42. | ( | 43. | ENT | 44. | Kin 4 | 45. | ENT |
| 46. | Kin 5 | 47. | ENT | 48. | Kin 6 | 49. | + | 50. | Kout 2 |
| 51. | + | 52. | MR | 53. | ) | 54. | HLT | 55. | Kout 4 |
| 56. | ) | 57. | X←→Y | 58. | × | 59. | Kout 1 | 60 | + |
| 61. | Kout 3 | 62. | × | 63. | Kout 5 | 64. | - | 65. | Kout 2 |
| 66. | × | 67. | Kout 6 | 68. | - | 69. | MR | 70. | Kin × 2 |
| 71. | × | 72. | Kout 6 | 73. | - | 74. | Kout 2 | 75. | ) |
| 76. | HLT | 77 | 0 | 78. | ) | 79. | Kin × 4 | 80. | 0 |
| 81. | ) | 82. | Kin × 5 | 83. | 0 | 84. | = | 85. | Kin × 6 |
| 86. | Kout 4 | 87. | Kin + 6 | 88. | Kout 5 | 89. | Kin + 6 | 90. | Kout 6 |
LRN 模式輸入程式(只供 fx-3800P使用,程式長度: 90步 )
| ENT | Min | Kin 3 | × | ENT |
| Kin 5 | ENT | Kin 4 | Kin 6 | ENT |
| Kin × 6 | Kin 1 | ENT | Kin 2 | - |
| ENT | Kin × 3 | X←→K3 | Kin - 6 | Kout 1 |
| × | Kout 5 | + | ( | Kout 6 |
| + | ( | Kout 5 | × | Kout 3 |
| - | Kout 2 | × | Kout 4 | + |
| ( | Kout 5 | + | ( | Kout 4 |
| × | ( | ENT | Kin 4 | ENT |
| Kin 5 | ENT | Kin 6 | + | Kout 2 |
| + | MR | ) | HLT | Kout 4 |
| ) | X←→Y | × | Kout 1 | + |
| Kout 3 | × | Kout 5 | - | Kout 2 |
| × | Kout 6 | - | MR | Kin × 2 |
| × | Kout 6 | - | Kout 2 | ) |
| HLT | 0 | ) | Kin × 4 | 0 |
| ) | Kin × 5 | 0 | = | Kin × 6 |
| Kout 4 | Kin + 6 | Kout 5 | Kin + 6 | Kout 6 |
| MODE . |
例題: 計算下列矩陣的特徵多項式。
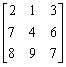
按 Prog 1 再按 2 EXE 1 EXE 3 EXE 7 EXE 4 EXE 6 EXE 8 EXE 9 EXE 7 EXE
(顯示x2的係數為13) EXE (顯示x的係數為35) EXE (顯示常數項為40)
所以特徵多項式是 –x3 + 13x2 + 35x + 40
註: 行列式的數值記存在K6。