三階矩陣乘法
程式編寫日期: 2006年3月17日 修改日期: 2008年1月3日
第一個程式可以計算一個 3 × 3 整數矩陣及另一個 3 × n矩陣的乘積,其中 n是正整數。 第二個及第三個程式沒有整數的限制,第二個程式較短,但準確度低一點,第三個程式準確度很高,但程式較長一點。
程式需要在 REG Quad 模式下執行,因此在輸入程式前請先按 Mode Mode 2 → 3 進入REG Quad模式。
注意: 藍色的英文字為統計模式中的變數(Σx³ 按 Shift 1 → → 1,Σy 按 Shift 1 → 2,Σxy 按 Shift 1 → 3),而 ³√是按shift x³,10x是按shift log。
第一個程式(整數版,128 byes)
Stat clear: ?→M: ³√(M-1 DT: ?→X: ?→Y: 1 , X + Y10x-6 DT:
?→M: 0 , M - Σy DT: ?→A: ?→B: ?→C: ?→D: ?→M: M ; 0 DT:
Lbl 0: ?→X: ?→Y: ?→M: Fix 0: Σxy: Rnd: Norm 1:
XΣx³ + YAns + M10x6(Σxy - Ans◢ XΣy + YA + MB◢ ; 0 DT:
XC + YD + MAns◢ Goto 0
程式限制: 第一個矩陣第二及第三個輸入的數據,絶對值必須為小於100000的整數。
第二個程式(小數精簡版,137 byes)
Stat clear: ?→M: ³√(M-1 DT: ?→M: 1 , M DT: ?→M:
?→A: 0 , A - Σy DT: ?→B: ?→C: ?→D: ?→X: ?→A:
³√M , X ; 0 DT: Lbl 0: ?→X: ?→Y: ?→M:
XΣx³ + YΣxy + MAns³◢ XΣy + YB + MC◢
DX + MA→X: Σy→M: ; 1 DT: Σy - M→M: ; -1 DT:
MY + X◢ ; 0 DT: Goto 0
程式限制: 程式雖然可以接受小數,但可能存在計算誤差,為了被免誤差出現,所以輸入的數值的絶對值不宜太大或太小,建議最大的絶對值小於106, 除了輸入0外,最小的位值為10-5。
第三個程式(小數及有效數字準確版,156 byes)
Stat clear: -1 DT: ?→M: 1 , M DT: ?→M: ³√M , 0 DT: ?→M:
0 , M - Σy DT: ?→A: ?→B: ?→M: ?→X: ?→C: ?→D: D10x60→D:
M10x-60 , X ; 0 DT: Lbl 0: ?→X: ?→Y: ?→M:
XΣxy + YΣx³ +MΣy◢ ; 0 DT: XA + YB + AnsM10x60◢
YC + DM10x-60→Y: Σy→M: ; 1 DT: Σy - M→M:
MX +Y◢ ; -1 DT: Goto 0
程式限制: 無特別限制。
例題: 計算下列矩陣的乘積:
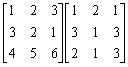
按 Prog 1 再按 1 EXE 2 EXE 3 EXE 3 EXE 2 EXE 1 EXE 4 EXE 5 EXE 6 EXE
(第一個矩陣,由左至右,上至下輸入)
1 EXE 3 EXE 2 EXE (輸入第二個矩陣,第一欄的數據)
(顯示13) EXE (顯示11) EXE (顯示31,這三個數值為答案的第一欄)
EXE 2 EXE 1 EXE 1 EXE (輸入第二個矩陣,第二欄的數據)
(顯示7) EXE (顯示9) EXE (顯示19,這三個數值為答案的第二欄)
EXE 1 EXE 3 EXE 3 EXE (輸入第二個矩陣,第三欄的數據)
(顯示16) EXE (顯示12) EXE (顯示37,這三個數值為答案的第三欄)
所以:
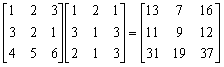
註1: 若果輸入的乘數矩陣大於或等於 3×4 矩陣時,執行程式有可能出現"Data Full",只要再按 AC 1 (即選用Edit OFF),程式可回復正常執行。
註2: 第二個程式輸入第四個數值時,不可以直接輸入分數,否則會出現Math ERROR,若要輸入分數請以除號代替分號輸入即可。