三階矩陣特徵多項式及特徵值

程式需要使用兩個程式組成(合共210 bytes)，程式第一部份用作計算三階陣的特徵多項式，而多項式的x³係數必為 -1。程式第二部份必須在第一個程式執行完成後才可以執行，用作計算三階矩陣的特徵值 Eigenvales (包括複數值)。

程式編寫日期: 2007年7月4日

程式第一需要在 SD 模式下執行，因此在輸入程式前請先按 Mode Mode 1 進入SD模式。

注意: 藍色的英文字為統計模式中的變數(n 按 shift 1 3 ，Σx為平均x 按 shift 1 2)

程式第一部份(111 bytes)

Stat clear: ?→A: ; A - 1 DT: ?→B: B DT:

?→C: ?→A: ?→B: ?→D: ?→X: ?→Y: ?→M:

nBM + AYC + XΣxD - YDn - MAΣx - XBC ; 0 DT:

DY - BM - nM - nB + ΣxA  +XC→C:

n+B+M→B◢ C◢ ; 0 DT: Ans→M

程式第二部份需要在 CMPLX 模式下執行，因此在輸入程式前請先按 Mode 2。

程式第二部份(99 bytes)

B┘3→B: BC┘2 + B³ + M┘2→M:

√(Ans² -  ( C┘3 + B²)³ M+:

Ansi => 2 ³√Abs M cos ( arg M ÷ 3) => Goto 0:

³√M + ³√( M + 2Ansi: Lbl 0: Ans + B→A◢

3B - Ans→M: M┘2 + √(AM + C + M²┘4 M-◢ M

例題: 計算下列矩陣的特徵多項式及特徵值。

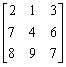
假設程式第一部分儲存在P1，程式第二部份儲存在P2。

按 Prog 1  再按 2 EXE 1 EXE 3 EXE 7 EXE 4 EXE 6 EXE 8 EXE 9 EXE 7 EXE

(顯示x²的係數為13) EXE (顯示x的係數為35) EXE (顯示常數項為40)

所以特徵多項式是  –x³ + 13x² + 35x + 40

程式第一部份執行完成後，

再按 Prog 2 (顯示第一個特徵值為 15.435)

EXE (顯示第二個特徵值實數部為 -1.2177)

再按 SHIFT Re<=>Im (顯示第二個特徵值虛數部為 1.0529 i)

EXE (顯示第三個特徵值實數部為 -1.2177)

再按 SHIFT Re<=>Im (顯示第三個特徵值虛數部為 - 1.0529 i)

返回 fx-3650P及SB185程式集

Stat clear: ?→M: M: ?→M: ³√ Ans , M DT:

?→C: ?→B: ?→A: ?→D: ?→X: ?→Y: ?→M:

Σx³AM + BYC + XΣyD - YDΣx³ - MBΣy - XAC ; 0 DT:

DY - AM - Σx³M - Σx³A + ΣyB  +XC→C:

Σx³+A+M→B◢ C◢ ; 0 DT: Ans→M